Probleme rezolvate de catre :
- Ginghina Cristian
- Onica Viorel
- Neculai Alexandru
- Anton Cosmin
1. Cate grafuri neorientate, distincte, cu 4 vârfuri, se pot construi? Două grafuri se consideră
distincte dacă matricele lor de adiacenţă sunt diferite. (4p.)
a. 24 b. 4 c. 46 d. 2 la puterea 6
2n(n-1)/2 => 24(4-1)/2 => 26
R: d
2.Prin înălţimea unui arbore cu rădăcină înţelegem numărul de muchii ale celui mai lung lanţ
format din noduri distincte care are una dintre extremităţi în rădăcina arborelui. Scrieţi care
este înălţimea şi care sunt frunzele arborelui descris prin următorul vector ”de taţi”:
1 2 3 4 5 6 7 8
(6,6,5,0,6,4,4,7).
INALTIME: Nivelul 4
FRUNZE: 1,2,3,8
3.Se consideră un graf orientat cu 6 noduri numerotate de la 1 la 6 şi cu mulţimea arcelor
formată doar din arcele:
- de la fiecare nod numerotat cu un număr neprim i (i>1) la toate nodurile numerotate cu
numere ce aparţin mulţimii divizorilor proprii ai lui i (divizori diferiţi de 1 şi de i)
- de la nodul numerotat cu 1 la nodul numerotat cu 6
- de la fiecare nod numerotat cu un număr prim i la nodul numerotat cu i-1
Pentru graful dat, care este lungimea celui mai mare drum, format doar din noduri distincte?
R: Cel mai lung drum format din noduri distincte este 6-3-2-1
4. Câte frunze are arborele cu rădăcină descris prin următorul vector ”de taţi”:
1 2 3 4 5 6 7 8 9 10 11
(6,5,5,2,0,3,3,3,8, 7, 7)? (4p.)
a. 1 b. 2 c. 5 d. 4
R: Nr. de frunze 5 (1,4,9,10,11)
5. Într-un graf neorientat cu 20 muchii, fiecare nod al grafului are gradul un număr nenul. Doar
patru dintre noduri au gradul un număr par, restul nodurilor având gradele numere impare.
Care este numărul maxim de noduri pe care poate să le aibă graful? (4p.)
a. 32 b. 36 c. 10 d. 16
R:36
6. Se consideră un arbore cu rădăcină în care doar 13 dintre nodurile sale au exact 2
descendenţi direcţi (fii), restul nodurilor având cel mult un descendent direct (fiu). Care este
numărul frunzelor arborelui?
R: 2*13
7. Se consideră un arbore cu 11 muchii. Care este numărul de noduri ale arborelui? (6p.)
R: n=m+1=> n=11+1 => n=12
8. Se consideră un graf neorientat G cu 12 noduri si 7 muchii. Care este numărul maxim de
componente conexe din care poate fi format graful G?
R: 8 componente conexe
9. Se consideră graful neorientat definit prin mulţimea vârfurilor {1,2,3,4,5,6} şi mulţimea
muchiilor {[1,2],[2,3],[3,4],[3,5],[4,5],[1,3],[2,6],[2,4],[4,6]}.
Care este numărul minim de muchii ce pot fi eliminate astfel încât graful parţial obţinut să
nu mai fie conex?
R: 2 muchii ([2,6] si [6,4] sau [3,5] si [4,5])
10. Se consideră graful orientat cu 6 noduri reprezentat prin matricea de
adiacenţă alăturată. Care este numărul tuturor grafurilor parţiale distincte
ale grafului dat? Doua grafuri parţiale sunt distincte dacă matricele lor de
adiacenţă sunt diferite.
0 1 0 1 0 1
0 0 0 0 1 0
0 0 0 0 0 0
0 0 0 0 1 0
0 0 0 0 0 1
0 0 1 0 0 0
R:
11. Se consideră graful orientat reprezentat prin listele de adiacenţă
alăturate. Câte noduri au gradul extern mai mare decât gradul
intern?
R:2
grEXTERN(1)=3, grINTERN(1)=1
grEXTERN(4)=1, grINTERN(4)=0
12. Se consideră un graf neorientat cu 50 noduri şi 32 muchii. Care este numărul maxim de
vârfuri cu gradul 0 pe care le poate avea graful? (4p.)
a. 45 b. 40 c. 41 d. 50
R: 41
Se deseneaza 10 noduri si se traseaza muchiile. =>50-9=41
13. Se consideră un graf orientat cu 6 noduri care are următoarele proprietăti:
- suma gradelor externe ale tuturor vârfurilor grafului este egală cu 6
- sunt numai 3 vârfuri care au gradul intern egal cu 1
Care este valoarea maximă pe care o poate avea gradul extern al unui vârf din graful dat?
R:: gradul extern este 4
14. Se consideră un graf neorientat cu 80 de noduri şi 3560 muchii. Care este numărul de
muchii ce pot fi eliminate astfel astfel încât graful parţial obţinut să fie arbore?
R:3481
15. Se consideră graful orientat reprezentat prin matricea de adiacenţă
alăturată. Care este lungimea maximă a unui drum, de la vârful 4 până
la vârful 6, format din vârfuri distincte două câte două (lungimea unui
drum este egală cu numărul de arce care compun acel drum)?
0 1 1 0 0 0
0 0 0 0 1 1
0 0 0 0 0 0
0 0 1 0 1 0
1 1 0 0 0 1
1 0 1 0 0 0
Raspuns: 5 4->5->1->2->6
16.Un graf orientat este reprezentat prin matricea de
adiacenţă alăturată. Care sunt nodurile pentru care gradul
interior este mai mare decât gradul exterior?
0 1 1 0 0 0
0 0 1 1 0 1
1 1 0 1 0 0
0 0 0 0 1 0
0 1 0 0 0 0
0 1 0 0 1 0
a. 2, 4, 5, 6 b. 2, 4, 5 c. 1, 4, 5 d. 1, 3, 6
Rezolvare:
Nodul: 1 gr. intern: 1, gr. extern: 2;
2 gr. intern: 4, gr. extern: 3;
3 gr. intern: 2, gr. extern: 3;
4 gr. intern: 2, gr. extern: 1;
5 gr. intern: 2, gr. extern: 1;
6 gr. intern: 1, gr. extern: 2;
Raspuns: b
17. Pentru arborele cu rădăcină având următorul vector de “de taţi”
tata=(2,0,2,3,2,3,4,4,3), care este rădăcina arborelui şi care sunt descendenţii
direcţi (fiii) ai nodului 3?
R:
Radacina: 2
Descedenti directi ai nodului 3: 4,6,9
18. Care este vectorul "de taţi" pentru arborele cu rădăcină
din figura alăturată?
a. 0 0 5 7 6 5 1 b. 1 0 0 7 6 5 0
c. 7 4 5 0 4 5 4 d. 7 4 5 0 4 5 7
R: c
19. Se consideră un graf neorientat cu 5 noduri, etichetate cu literele a, b, c, d, e, în care orice
nod etichetat cu o vocală este adiacent cu toate nodurile etichetate cu consoane, iar orice
nod etichetat cu o consoană este adiacent cu toate nodurile etichetate cu vocale. Câte
muchii are acest graf?
a. 12 b. 6 c. 4 d. 3
R: b:6 muchii
20. Care sunt etichetele nodurilor de tip frunză ale arborelui cu rădăcină, având 7 noduri,
numerotate de la 1 la 7, şi următorul vector “de taţi”: (5,1,5,1,0,7,5)?
R: Nodurile de tip frunza ale arborelui sunt 2,3,4 si 6 deoarece aceste noduri nu se gasesc in vectorul tata, ele nemaiavand descendeti.
21. Câţi fraţi are nodul 1 din arborele cu rădăcină cu 7 noduri, numerotate de la 1 la 7, având
următorul vector ”de taţi”: (5,1,5,1,0,7,5)?
R: Nodul 1 din arbore are 2 frati si anume nodul 3 si nodul 7, deoarece aceste noduri au acelasi tata ca si nodul 1, respectiv nodul 5
22. Se consideră graful neorientat cu 8 noduri, numerotate de la 1 la 8, şi muchiile [1,2],
[1,6], [1,7], [2,3], [2,6], [3,6], [3,4], [4,5], [4,8], [5,6], [7,8]. Care este
gradul minim al unui nod din acest graf? Care sunt nodurile care au acest grad minim?
R: (1,2,3,4,5,6,7) pentru ca graful este conex si daca mutam un nod se poate face ciclu
Probleme realizate de catre :
- Constantinescu Florin
- Totoc Traian
- Tigau Adrian
1. Dacă n este un număr impar mai mare decât 2, un graf neorientat cu n noduri, în care fiecare nod este adiacent cu exact n-1 noduri, este întotdeauna :
a. arbore
b. graf eulerian
c. graf neconex
d. graf aciclic (graf care nu conţine niciun
ciclu)
Raspuns: b. graf eulerian
Varianta 17
3. Care este gradul maxim posibil şi care este gradul minim posibil pentru un nod dintr-un arbore cu n noduri?
Raspuns : Gradul maxim este 4,iar gradul minim este 1
Varianta 18
3. Un arbore binar este un arbore cu rădăcină în care fiecare nod are cel mult 2 descendenţi direcţi (fii). Înălţimea unui arbore este reprezentată de numărul maxim de muchii ale unui lanţ elementar ce uneşte rădăcina cu un vârf terminal (frunză).
Pentru un arbore binar cu exact 8 noduri, care este înălţimea minimă posibilă şi care este numărul de noduri terminale (frunze) în acest caz?
Raspuns: Inaltimea minima este 3 ,iar numarul de frunze este 4
Varianta 19
1. Un graf neorientat este complet dacă oricare două noduri distincte ale sale sunt adiacente. Care este numărul de muchii care trebuie eliminate dintr-un graf neorientat, complet, cu 7 noduri, astfel încât graful parţial obţinut să fie arbore?
a. 15
b. 1
c. 6
d. 21
Raspuns: a. 15
Varianta 20
1. Matricea de adiacenţă a unui graf neorientat G are numărul valorilor de 1 egal cu jumătate din numărul valorilor de 0. Care dintre numerele de mai jos poate fi numărul de noduri ale grafului G?
a. 12
b. 14
c. 11
d. 13
Raspuns: a. 12
Varianta 21
2. Într-un graf orientat cu 7 noduri suma gradelor interioare ale tuturor nodurilor este egală cu 10. Care este valoarea sumei gradelor exterioare ale tuturor nodurilor?
a. 5
b. 20
c. 10
d. 1
Raspuns: c. 10 
Varianta 22
4. Într-un graf neorientat cu 10 noduri, numerotate de la 1 la 10, există câte o muchie între oricare două noduri numerotate cu numere consecutive şi câte o muchie între nodul numerotat cu 10 şi fiecare dintre celelalte noduri. Câte subgrafuri cu exact 3 noduri, toate adiacente două câte două, are graful dat?
Raspuns: 8 
Varianta 23
3. Care sunt nodurile care au exact 2 descendenţi pentru un arbore cu rădăcină, cu 7 noduri, numerotate de la 1 la 7, dat de vectorul de ”taţi”: (3,3,0,1,2,2,4)?
Raspuns: 2,3
Varianta 24
2. Care din următoarele proprietăţi este adevărată pentru un graf orientat cu n vârfuri şi n arce (n>3) care are un circuit de lungime n:
a. există un vârf cu gradul n-1
b. pentru orice vârf gradul intern şi gradul extern sunt egale
c. graful nu are drumuri de lungime strict mai mare decât 2
d. gradul intern al oricărui vârf este egal cu 2
Raspuns: b. pentru orice vârf gradul intern şi gradul extern sunt egale
Varianta 25
2. Un graf neorientat cu 8 noduri are gradele nodurilor egale cu 1,2,4,2,3,2,1,x. Pentru
ce valoare a lui x graful este arbore?
a. x=1
b. x<3
c. x>3
d. nicio valoare
Raspuns: d. nicio valoare
Varianta 26
1. Pentru graful neorientat din figura alăturată, care este numărul de
muchii ale celui mai lung lanţ, format din noduri distincte, ce are
ca extremităţi nodurile 1 şi 3?
a. 2 b. 3 c. 1 d. 4
Raspuns: d. 4 (1,2,4,5,3)
2. Care este nodul ce poate fi ales ca rădăcină a arborelui din figura
alăturată, astfel încât fiecare nod care nu este de tip frunză să aibă
un număr impar de descendenţi direcţi (fii) ?
a. 3 b. 4 c. 6 d. 1
Raspuns: c. 6
Varianta 27
1. Care este numărul minim de arce ce trebuie adăugate în graful orientat
din figura alăturată astfel încât fiecare vârf să aparţină unui circuit ?
a. 1 b. 2 c. 3 d. 4
Raspuns: a. 1
2. Care este numărul nodurilor de tip frunză din arborele cu rădăcină, cu 8 noduri, numerotate de la 1 la 8, reprezentat prin vectorul ”de taţi” (2,0,6,2,4,4,5,5)?
a. 3 b. 4 c. 5 d. 2
Raspuns: b. 4
Varianta 28
1. Care este numărul minim de muchii ce pot fi eliminate din graful
alăturat astfel încât în graful parţial rezultat să existe exact un vârf de
grad 0? (6p.)
a. 1 b. 3 c. 2 d. 5
Raspuns: b. 3
2. Într-un arbore cu rădăcină nivelul unui nod este egal cu lungimea lanţului format din noduri distincte care uneşte rădăcina cu acel nod. Rădăcina se află pe nivelul 0. Dacă toate frunzele se află pe nivelul 3 şi oricare nod neterminal aflat pe un nivel k are exact k+1 descendenţi direcţi (fii), care este numărul de noduri din acest arbore ? (4p.)
a. 8 b. 9 c. 10 d. 6
Raspuns: c. 10
Varianta 29
1. Care este numărul maxim de noduri de grad 3 într-un graf neorientat cu 5 noduri?
a. 4 b. 5 c. 3 d. 2
Raspuns: a. 4
2. Într-un arbore cu rădăcină nivelul unui nod este egal cu lungimea lanţului
format din noduri distincte care uneşte rădăcina cu acel nod. Care dintre
noduri trebuie ales ca rădăcină în arborele din figura alăturată astfel încât
pe fiecare nivel să se găsească un număr impar de noduri?
a. 2 b. 3 c. 6 d. 4
Raspuns: d. 4
Varianta 30
1. Care este numărul minim de muchii ce trebuie mutate în graful din
figura alăturată astfel încât acesta să fie conex şi fiecare nod să
aparţină unui ciclu?
a. 0 b. 1 c. 2 d. 3
Raspuns: b. 1
3. Care sunt nodurile de tip frunză din arborele alăturat dacă se alege ca
rădăcină nodul 6?
Raspuns: 5,4,3,2
Varianta 31
1. Se consideră graful neorientat cu 7 noduri, numerotate de la 1 la 7, şi muchiile[1,3], [2,3], [3,4], [3,5], [5,4], [1,2], [2,5], [2,4], [6,7], [3,6]. Care dintre următoarele succesiuni de noduri reprezintă un lanţ care trece o singură dată prin toate nodurile grafului?
a. (1, 2, 3, 4, 5, 6, 7) b. (4, 5, 3, 6, 7)
c. (7, 6, 3, 5, 4, 2, 1) d. (1, 3, 5, 4, 2, 3, 6)
Raspuns: c. (7, 6, 3, 5, 4, 2, 1)
2. Un arbore cu 11 noduri, numerotate de la 1 la 11, este memorat cu ajutorul vectorului de taţi t=(2,5,5,3,0,2,4,6,6,2,3). Mulţimea tuturor ascendenţilor nodului 8 este:
a. {1, 2, 5, 6, 10} b. {6, 2, 5} c. {6} d. {5, 2}
Raspuns: b. {6, 2, 5}
Varianta 32
1. Un graf orientat este memorat cu ajutorul listelor de
adiacenţă scrise alăturat. Nodurile care au gradul exterior
egal cu 2 sunt: 1:(5,6) 2:(1,5,4) 3:(1,5) 4:(1,2) 5:(2) 6:(2,4,5)
a. 2 şi 5 b. 1,3 şi 4 c. 6 d. 2 şi 3
Raspuns: b. 1,3 şi 4
2.Graful neorientat cu 8 noduri, numerotate de la 1 la 8, este
reprezentat cu ajutorul matricei de adiacenţă alăturate. Pentru acest
graf este adevărată afirmaţia:
a. Graful este hamiltonian b. Graful nu are noduri de grad 0
c. Gradul maxim al unui nod este 3 d. Graful are trei componente conexe
Raspuns: d. Graful are trei componente conexe 
Realizat de catre :
- Apostolache Diana Raluca
- Badea Cristian
- Focsa Alexandru
- Onea Cristian
a. vârful numerotat cu 6 aparţine unui circui
b. vârful numerotat cu 1 are gradul extern 0
c. gradul intern al vârfului numerotat cu 4 este 1
d. graful nu are circuite
orientat dat prin matricea de adiacenţă alăturată? 1 0 1 0 1 1
Două circuite sunt distincte dacă diferă prin cel 0 0 0 0 0 0
puţin un arc.(4p.) 0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 1 1 0
a. 0 b. 1 c. 2 d. 3
Două circuite sunt distincte dacă diferă prin cel 0 0 0 0 0 0
puţin un arc.(4p.) 0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 1 1 0
a. 0 b. 1 c. 2 d. 3
Raspuns : 6 (adica 4, 6, 7, 8, 9, 0)
a. 4, 2, 6, 4, 2
b. 2, 2, 1, 2, 2
c. 1, 1, 1, 1, 1
d. 4, 3, 3, 4, 4
5. Care este numărul maxim de muchii pe care îl poate avea un graf neorientat cu 6 noduri şi 3 componente conexe?
Raspuns: 6 muchii
6. Se consideră graful neorientat din figura alăturată. Care este numărul minim de muchii ce se pot elimina astfel încât graful parţial obţinut să aibă exact 3 componente conexe? (4p.)
a. 2 b. 4 c. 1 d. 3a. 2, 3, 1, 1, 1
b. 2, 2, 6, 5, 1
c. 1, 0, 1, 1, 1, 1
d. 1, 1, 0, 2, 1
8. Se consideră un graf neorientat cu 10 vârfuri astfel încât între oricare două vârfuri distincte există muchie. Câte lanţuri distincte de lungime 3 există între vârful 2 şi vârful 4? Lungimea unui lanţ este egală cu numărul de muchii din care este compus. Două lanţuri sunt distincte dacă diferă prin cel puţin o muchie. :
a. 90 b. 28 c. 45 d. 56
9. Se consideră graful orientat din figura alăturată. Câte dintre vârfurile grafului au gradul intern egal
cu gradul extern?
a. 3 b. 2 c. 1 d. 4
Varfurile care au gradul intern egal cu cel extern sunt: 1, 3, 5.

10. Variabila n memorează un număr natural nenul. Care este numărul total de grafuri orientate distincte cu n noduri? Două grafuri orientate sunt distincte dacă matricele lor de adiacenţă sunt diferite. (4p.)
a. 4n(n-1)/2 b. 3 n(n-1)/2 c. 4 n(n-1)d. 2 n(n-1)/2
Exemplu: Luam graful orientat cu 2 noduri.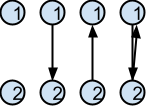
a. 90 b. 28 c. 45 d. 56
9. Se consideră graful orientat din figura alăturată. Câte dintre vârfurile grafului au gradul intern egal
cu gradul extern?
a. 3 b. 2 c. 1 d. 4
Varfurile care au gradul intern egal cu cel extern sunt: 1, 3, 5.
10. Variabila n memorează un număr natural nenul. Care este numărul total de grafuri orientate distincte cu n noduri? Două grafuri orientate sunt distincte dacă matricele lor de adiacenţă sunt diferite. (4p.)
a. 4n(n-1)/2 b. 3 n(n-1)/2 c. 4 n(n-1)d. 2 n(n-1)/2
Exemplu: Luam graful orientat cu 2 noduri.
Apoi inlocuim n cu nr. de noduri (care sunt 2). 42(2-1)/2= 42*1/2= 41 = 4, adica numarul de cazuri.Un graf orientat complet cu n noduri are n*(n-1) muchii. Numărul de submulţimi din mulţimea muchiilor este 2.
11. Care este numărul maxim de muchii pe care-l poate avea un graf neorientat cu 6 noduri, care nu este conex? (4p.)
a. 4 b. 15 c. 12 d. 10
12. Fie T un arbore cu rădăcină. Arborele are 8 noduri numerotate de la 1 la 8 şi este descris prin următorul vector „de taţi”: (4,1,6,0,1,1,4,7). Care sunt frunzele arborelui? (6p.)
Raspuns: 1 2 3 4 5 6 7 8 , iar arborele va arata astfel:
4 1 6 0 1 1 4 7
- plecam cu numarul care ii corespunde (este deasupra) lui 0;
- apoi ne uitam care numere ii corespund deasupra cifrei 4;
- apoi facem pentru fiecare cifra in parte, iar numere care nu au descendenti se numesc „frunze” : 2, 3, 5, 8.
a. G are cel puţin un ciclu;
b. G este conex;
c. G are gradele tuturor nodurilor numere pare;
d. G nu poate avea noduri cu gradul 0.
14. Fie T un arbore cu rădăcină. Arborele are 8 noduri numerotate de la 1 la 8 şi este descris prin următorul vector „de taţi”: (3,5,0,3,3,5,5,5). Care este nodul cu cei mai mulţi descendenţi direcţi (fii)? (6p.)
Raspuns: 1 2 3 4 5 6 7 8 , arborele este:
15. Dacă G este un graf neorientat cu 11 noduri şi 13 muchii, fără noduri cu gradul 0, atunci
numărul maxim de componente conexe pe care le poate avea graful este: (4p.)
a. 2 b. 4 c. 3 d. 5

16. Fie n un număr natural, n>4. Orice graf neorientat cu n noduri şi n muchii : (4p.)
a. are gradele tuturor nodurilor numere pare
b. este conex
c. are cel puţin un ciclu
d. este arbore.
17. Fie T un arbore cu rădăcină. Arborele are 8 noduri numerotate de la 1 la 8 şi este descris prin următorul vector „de taţi”: (4,5,0,3,4,5,4,5). Care sunt frunzele arborelui?
Raspuns: 1 2 3 4 5 6 7 8 , arborele este:
numărul maxim de componente conexe pe care le poate avea graful este: (4p.)
a. 2 b. 4 c. 3 d. 5
16. Fie n un număr natural, n>4. Orice graf neorientat cu n noduri şi n muchii : (4p.)
a. are gradele tuturor nodurilor numere pare
b. este conex
c. are cel puţin un ciclu
d. este arbore.
17. Fie T un arbore cu rădăcină. Arborele are 8 noduri numerotate de la 1 la 8 şi este descris prin următorul vector „de taţi”: (4,5,0,3,4,5,4,5). Care sunt frunzele arborelui?
Raspuns: 1 2 3 4 5 6 7 8 , arborele este:
4 5 0 3 4 5 4 5
Frunzele arborelui sunt: 1, 2, 6, 7, 8.
18. Dacă G este un graf neorientat cu 8 noduri şi 2 componente conexe, atunci graful are cel mult: (4p.)
a. 28 de muchii
b. 12 muchii
c. 21 de muchii
d. 16 muchii
Raspuns: 2 componente conexe : 1-2-3-4-5-6-7 si 8 ;muchii: (7*6)/2=21.
19. Dacă T este un arbore cu rădăcină cu 100 de noduri, care este numărul minim de frunze pe care le poate avea T?
Raspuns: 1
Frunzele arborelui sunt: 1, 2, 6, 7, 8.
18. Dacă G este un graf neorientat cu 8 noduri şi 2 componente conexe, atunci graful are cel mult: (4p.)
a. 28 de muchii
b. 12 muchii
c. 21 de muchii
d. 16 muchii
Raspuns: 2 componente conexe : 1-2-3-4-5-6-7 si 8 ;muchii: (7*6)/2=21.
19. Dacă T este un arbore cu rădăcină cu 100 de noduri, care este numărul minim de frunze pe care le poate avea T?
Raspuns: 1
muchii pe care le poate avea graful
neorientat G, dacă graful din figura
1 reprezintă un subgraf al lui G,
iar graful reprezentat în figura 2
este graf parţial al lui G?(4p.)
a.8 b.7 c.5. d.6
(Figura 1) (Figura 2)
Raspuns:

21. Se consideră un arbore cu rădăcină, cu 100 noduri, numerotate de la 1 la 100. Dacă nodul 13 are exact 14 fraţi şi nodul 100 este tatăl nodului 13, care este numărul total de
descendenţi direcţi (fii) ai nodului 100?
Raspuns: 15 fii.
Daca nodul 13 este fiu al nodului 100 si are 14 fii, atunci numarul total de descendenti este 15. (14+1=15).
Raspuns:
21. Se consideră un arbore cu rădăcină, cu 100 noduri, numerotate de la 1 la 100. Dacă nodul 13 are exact 14 fraţi şi nodul 100 este tatăl nodului 13, care este numărul total de
descendenţi direcţi (fii) ai nodului 100?
Raspuns: 15 fii.
Daca nodul 13 este fiu al nodului 100 si are 14 fii, atunci numarul total de descendenti este 15. (14+1=15).
a.Graful parţial al lui G obţinut prin eliminarea
muchiilor: [5,6], [2,5], [2,3], [2,10],[10,8],[1,3], este
un arbore.
b. Graful conţine un singur ciclu.
c. Cel mai lung lanţ, care conţine numai noduri
distincte, are lungimea 8.
d. Numărul nodurilor de grad par este egal cu
numărul nodurilor de grad impar.
23. Se consideră graful orientat G, cu 6 vârfuri, definit cu ajutorul listelor de adiacenţă alăturate.Construiţi matricea de adiacenţă corespunzătoare grafului orientat G1, cu 6 vârfuri, în care există arc între vârfurile distincte i şi j dacă şi numai dacă în graful G există cel puţin un drum de la i la j.(6p.)
1: 2 6 Raspuns: 0 1 1 0 0 1
2: 3 0 1 0 0 0 0
3: 0 0 0 0 0 0
4: 3 0 0 1 0 0 0
5: 4 6 0 0 1 0 0 0
6: 3 0 0 1 0 0 0
24. Se consideră un arbore G, cu rădăcină, memorat cu ajutorul vectorului de taţi următor:
T=(2,0,4,2,4,7,2). Care dintre următoarele afirmaţii este adevărată? (4p.)
a. Nodurile 1,4 şi 6 sunt fraţi.
b. G este conex şi prin eliminarea unei muchii oarecare din G, graful obţinut nu este conex.
c. Prin eliminarea muchiei [6,7] se obţine un graf parţial, conex.
d. Arborele G are 5 frunze.
1: 2 6 Raspuns: 0 1 1 0 0 1
2: 3 0 1 0 0 0 0
3: 0 0 0 0 0 0
4: 3 0 0 1 0 0 0
5: 4 6 0 0 1 0 0 0
6: 3 0 0 1 0 0 0
24. Se consideră un arbore G, cu rădăcină, memorat cu ajutorul vectorului de taţi următor:
T=(2,0,4,2,4,7,2). Care dintre următoarele afirmaţii este adevărată? (4p.)
a. Nodurile 1,4 şi 6 sunt fraţi.
b. G este conex şi prin eliminarea unei muchii oarecare din G, graful obţinut nu este conex.
c. Prin eliminarea muchiei [6,7] se obţine un graf parţial, conex.
d. Arborele G are 5 frunze.
25. Câte vârfuri ale grafului din figura alăturată, au gradul interior mai mare decât gradul exterior? (6p.)
Raspuns: 3 (adica varfurile 3, 5 si 6)
!!Sunt 2 (3 si 5) dar la varinatele de raspuns arata ca sunt 3 (3,5,6).
26. Se consideră un graf neorientat dat prin listele de adiacenţă alăturate.Care este numărul maxim de muchii care pot fi eliminate din graf astfel încât graful parţial rezultat să fie conex ? (6p.)
1: 2 3
2: 1 3 4
3: 1 2 4 5
4: 2 3 5
5: 3 4
Raspuns: 3
27. Într-un graf orientat G cu 6 vârfuri numerotate cu numere distincte de la 1 la 6, există arc de la i la j dacă şi numai dacă i<j şi j-i>1. Câte vârfuri din graf au gradul interior maimare decât gradul exterior?
Raspuns: 3
1: grad int: 5, grad ext: 2;
2: grad int: 5, grad ext: 2;
3: grad int: 4, grad ext: 3;
4: grad int: 3, grad ext: 4;
5: grad int: 2, grad ext: 5;
6: grad int: 1, grad ext: 5;
-muchiile de la 1 la 5, sunt datorita conditiei i<j (ex:1<2; 2<3), iar restul sunt datorita conditiei j-i>1(ex: 6-1=5>1)
Raspuns: 3
1: grad int: 5, grad ext: 2;
2: grad int: 5, grad ext: 2;
3: grad int: 4, grad ext: 3;
4: grad int: 3, grad ext: 4;
5: grad int: 2, grad ext: 5;
6: grad int: 1, grad ext: 5;
-muchiile de la 1 la 5, sunt datorita conditiei i<j (ex:1<2; 2<3), iar restul sunt datorita conditiei j-i>1(ex: 6-1=5>1)
Realizat de catre :
- Balan Ana Maria
- Dunac Cristiana
- Lazar Maricel
- Enache Marian
Varianta 36
3. Se consideră un graf neorientat cu 7 noduri numerotate de la 1 la 7 şi muchiile[1,2],[1,3],[2,3],[2,4],[2,5],[2,6],[4,6],[5,7],[6,7]. Care este numărul minim de muchii care trebuie adăugate pentru ca acest graf să devină eulerian?
Graficul Eulerian este un graf care contine un ciclu eulerian (un ciclu simplu ce contine toate muchiile grafului).
Raspuns: 3, ([2,7],[1,7],[1,6])
4. Câte muchii trebuie eliminate dintr-un graf neorientat complet cu 20 de noduri, pentru ca acesta să devină arbore? Un graf este complet dacă oricare două noduri distincte sunt adiacente.
Raspuns: 171 (20*19/2 – 19=171)
Varianta 37
3. Se consideră un graf orientat cu 5 vârfuri reprezentat în figura alăturată. Care este matricea de adiacenţă corespunzătoare grafului?
Matricea de adiacentã asociatã unui graf neorientat cu n noduri se defineste astfel: A = (ai j) n x n .
Raspuns:
4. Scrieţi care este gradul intern al vârfului 5 şi gradul extern al vârfului 1.
Raspuns: 2 si 3
Varianta 38
3. Care este numărul minim de muchii care trebuie eliminate astfel încât graful să aibă 3
componente conexe?
Următorii doi itemi se referă la un graf neorientat cu 7 noduri, numerotate de la 1 la 7 şi muchiile:
[1,5], [2,3], [2,4], [2,5], [3,4], [4,5], [4,7], [5,6], [5,7].
Raspuns: 2 ([1,5],[5,6])
4. Câte cicluri elementare distincte există în graf? Două cicluri sunt distincte dacă diferă prin cel puţin o muchie.
Raspuns: 4.
Varianta 39
1. Stabiliţi care dintre următorii vectori este vector de ”taţi” pentru arborele cu 7 noduri, numerotate de la 1 la 7, cu rădăcina 1, reprezentat prin matricea de adiacenţă alăturată:
0 1 0 0 1 0 0
1 0 1 1 0 0 0
0 1 0 0 0 0 0
0 1 0 0 0 0 0
1 0 0 0 0 1 1
0 0 0 0 1 0 0
0 0 0 0 1 0 0
a. (1, 0, 2, 2, 1, 5, 5) b. (0, 1, 2, 2, 1, 5, 5)
c. (3, 1, 0, 2, 1, 5, 6) d. (2, 1, 0, 2, 1, 5, 2)
Raspuns: b.(0, 1, 2, 2, 1, 5, 5)
Varianta 40
1. Se consideră vectorul de ”taţi" al unui arbore cu rădăcină t=(3,4,0,3,3,5) ale cărui
noduri sunt numerotate de la 1 la 6. Alegeţi afirmatia corectă:
a. nodurile 4 şi 6 sunt noduri de tip frunză(fiu) b. nodul 3 are un singur descendent direct
c. nodul 6 este tatăl nodului 5 d. nodurile 1, 2, 6 sunt noduri de tip frunză
1 2 3 4 5 6
3 4 0 3 3 5
R: d. nodurile 1, 2, 6 sunt noduri de tip frunză 
3. Se consideră un graf neorientat cu 8 noduri, numerotate de la 1 la 8, şi muchiile [1,5],[1,6], [2,6], [3,4], [3,6], [3,7], [4,6], [6,8], [7,8]. Dacă se elimină nodul 6 şi toate muchiile incidente cu acesta câte componente conexe va avea subgraful rezultat?
Un graf G=(V, E)este conex daca pentru orice pereche x,y de noduri din V exista un lant de la x la y (implicit si de la y la x).
Se numeste subgraf al unui graf G = (X, U) un graf orientat iar arcele din multimea V sunt toate arcele din multimea U care au ambele extremitãti în multimea Y.
R: 3.
.
Varianta 41
1. Câte dintre vârfurile grafului neorientat G, reprezentat prin matricea de
adiacenţă alăturată, au gradul un număr par?
0 1 0 0 1
a. 1 b. 3 c. 2 d. 5 1 0 1 1 0
0 1 0 1 1
0 1 1 0 1
1 0 1 1 0
R: a. 1
3. Pentru reprezentarea unui arbore cu radacină cu 10 noduri, etichetate cu numere naturale de la 1 la 10, se utilizează vectorul de taţi: TATA=(4, 8, 8, 0, 10, 4, 8, 6, 2, 6). Care sunt frunzele arborelui?
1 2 3 4 5 6 7 8 9 10
4 8 8 0 10 4 8 6 2 6
R: 5 : ( 1,7,9,3,5 )
Varianta 42
1. Câte dintre vârfurile grafului neorientat G, reprezentat prin matricea de adiacenţă alăturată, au gradul 0 ?
a. 2 b. 1 c. 3 d. 0
R: a. 2
3. Pentru reprezentarea unui arbore cu radacină cu 9 noduri, etichetate cu numere naturale de la 1 la 9, se utilizează vectorul de “taţi”: T=(5,0,2,7,3,3,2,4,7). Din câte muchii este format un lanţ alcătuit din noduri distincte,lanţ de lungime maximă, în arborele dat?
1 2 3 4 5 6 7 8 9
5 0 2 7 3 4 2 4 7
R: 6 [ 8,4,7,2,3,5,1 ]
Varianta 43
1. Un graf neorientat este reprezentat prin matricea de adiacenţă alăturată. Câte grafuri parţiale distincte, formate doar din noduri cu gradul egal cu 2, se pot obţine din graful dat? Două grafuri sunt distincte dacă matricele lor de adiacenţă diferă.
a. 2 b. 1 c. 3 d. 0 0 1 0 0 1
1 0 1 1 0
0 1 0 1 1
R: a. 0 1 1 0 1
1 0 1 1 0
3. Pentru reprezentarea unui arbore cu rădăcină cu 10 noduri, etichetate cu numere naturale de la 1 la 10, se utilizează vectorul de taţi: TATA=(4, 8, 8, 0, 10, 4, 8, 6, 2, 6).Care este rădăcina arborelui şi câte frunze are acesta?
1 2 3 4 5 6 7 8 9 10
4 8 8 0 10 4 8 6 2 6
R - radacina: 4
- 5 frunze: 1,5,9,3,7.
Varianta 45
1). Graful neorientat G este dat prin matricea de adiacenţă alăturată.
Câte vârfuri ale grafului G au gradul 1?
0 0 0 0 1
0 0 1 1 0
0 1 0 1 1
0 1 1 0 1
1 0 1 1 0
a. 1 b. 2 c. 3 d. 0
Raspuns: a.1
3). Pentru reprezentarea unui arbore cu rădăcină cu 9 noduri, etichetate cu numere naturale de la 1 la 9, se utilizează vectorul de „taţi”: T=(2,0,1,7,3,1,2,4,1). Care sunt
descendenţii direcţi ai rădăcinii şi câte frunze are arborele dat?
Raspuns: Descendenti directi: 7,1
Frunze: 4
Varianta 46
1). Care dintre următoarele propoziţii este falsă pentru graful orientat G,
dat prin matricea de adiacenţă alăturată?
0 1 1 0 0
0 0 1 1 0
0 0 0 1 1
1 1 0 0 0
0 0 0 1 0
a. există cel puţin un nod în graful G care
are gradul intern egal cu cel extern
b. graful G nu are circuite
c. există cel puţin un drum între oricare
două noduri ale grafului G
d. graful G are 9 arce
Raspuns: b.graful G nu are circuite
3). Câte frunze are arborele cu rădăcină cu 9 noduri, numerotate de la 1 la 9, al cărui vector „de taţi” este (6, 6, 8, 8, 7, 7, 0, 7, 7)?
Raspuns: 6 frunze.
Varianta 47
1). Care dintre următorii vectori NU poate reprezenta vectorul „de taţi” al unui arbore cu
rădăcină, cu 5 noduri, numerotate de la 1 la 5?
a. 3 1 0 1 2 b. 2 0 1 1 2 c. 3 4 0 2 3 d. 4 1 1 0 2
a. 
b. 
c.
Raspuns: c. 3 4 0 2 3
Raspuns: c. 3 4 0 2 3
d. .
Varianta 48
3). Care este lungimea celui mai scurt drum de la nodul 1 la nodul 5 pentru graful orientat din figura alăturată?
Raspuns: 3 (1,2,6,5 sau 1,4,6,5)
1.Se consideră graful neorientat cu 6 noduri, definit cu ajutorul listelor de adiacenţă alăturate. Care dintre mulţimile următoare de noduri are toate elementele extremităţi ale unor lanţuri de lungime 2 cu cealaltă extremitate în nodul 5?
1: 4,5,6
2: 5
3: 4
4: 1,3
5: 1,2,6
6: 1,5
a. {1,4,6} b. {2} c. {3} d. {2,6}
Multimea care are toate elementele extremitati ale unor lanturi de lungime 2 cu cealalta extremitate in nodul 5 este {1,4,6}.
2. Un arbore cu rădăcină are nodurile numerotate de la 1 la 18 şi este reprezentat prin
vectorul de taţi t:(8,8,0,3,4,3,4,7,1,2,3,3,7,8,3,5,6,8). Numărul tuturor
descendenţilor nodului 3 este egal cu:
a.3 b.6 c.17 d.18
Numarul descendentilor nodului 3 este 17.
3. Graful neorientat cu 60 de noduri, numerotate de la 1 la 60, are numai muchiile [1,60],
[60,20], [2,30] şi [4,30]. Numărul componentelor conexe ale grafului este egal cu:
a.3 b.56 c.54 d.0
Numarul componentelor conexe este 54 deoarece 1,60,20 si 2,30,4 reprezinta 2
componente conexe iar restul punctelor sunt considerate si ele tot component conexe.
4. Într-un arbore cu rădăcină cu 10 noduri, numerotate de la 1 la 10, nodul 10 este rădăcină,
iar între celelate noduri există relaţia: nodul cu numărul i+1 este tatăl celui cu numărul i,
pentru i∈{1,2,3,4,5,6,7,8,9}. Vectorul de taţi al arborelui astfel definit, este: (4p.)
a. (0,1,2,3,4,5,6,7,8,9) b. (1,2,3,4,5,6,7,8,9,0)
c. (2,3,4,5,6,7,8,9,10,0) d. (9,8,7,6,5,4,3,2,1,0)
Vectorul de tati este (2,3,4,5,6,7,8,9,10,0) deoarece pentru i=1=>i+1=2 care este tata pentru 1;pentru i=2=>2+1=3,tata pentru 2;pentru i=3=>3+1=4,tata pentru 3 etc.
5. Se consideră graful neorientat cu mulţimea nodurilor {1,2,3,4,5,6,7,8} şi mulţimea
muchiilor {[1,2], [2,3], [2,4], [4,7], [2,6], [1,5], [5,6], [6,8], [7,8]}.
Pentru a trasforma graful într-un arbore, putem elimina: (4p.)
a. muchiile [1,5] şi [1,2] b. muchia [5,6]
c. nodul 3 d. muchiile [2,6] şi [4,7]
Pentru a avea un arbore trebuie sa eliminam muchia [5,6].
6. Graful orientat G este reprezentat prin matricea de adiacenţă alăturată.
Câte vârfuri din graful dat au gradul interior egal cu gradul exterior?
0 1 0 0 1
1 0 1 0 0
0 0 0 1 1
0 1 0 0 1
1 0 0 0 0
a.2 b.1 c.3 d.0
Gradu exterior este multimea arcelor care pleaca din varful respective,iar gradul interior este multimea arcelor care au ca extremitate finala acel varf.Prin urmare nodul 1 are gradul exterior 2 iar cel interior 2,nodul 2 are gradul exterior 2 si cel interior 2,nodul 3 are gradul exterior 2 iar cel interior 1,nodul 4 are gradul exterior 2 iar gradul interior 1 si nodul 5 are gradul exterior 1 si gradul interior 3.
Deci numarul varfurilor care au gradul exterior egal cu gradul interior este 2.
7. Pentru reprezentarea unui arbore cu radacină cu 9 noduri, etichetate cu numere naturale de la 1 la 9, se utilizează vectorul de „taţi”: T=(7,0,2,7,6,2,3,6,5). Care sunt nodurile
arborelui ce au exact 2 descendenţi direcţi (fii)?
Nodurile care au exact 2 descendenti sunt 2,6,7.
Rezolvat de catre :
- Chirila Alin
- Hancianu George
Varianta 81
2. Care dintre următoarele afirmaţii este adevărată pentru graful neorientat având mulţimea
nodurilor X={1,2,3,4,5} şi mulţimea muchiilor U={[1,2], [1,5], [2,3], [2,4],
[3,4], [4,5]}?
a. Este graf hamiltonian, dar nu este eulerian.
b. Este graf eulerian, dar nu este hamiltonian.
c. Este şi graf hamiltonian şi graf eulerian.
d. Nu este graf hamiltonian, şi nici nu este graf eulerian
.
Raspuns: A
Varianta 82:
1. Se consideră graful orientat cu nodurile numerotate de la 1 la 5 şi arcele (1,2), (1,5),
(2,1), (2,3), (2,5), (3,4), (5,2), (5,4). Care este lungimea maximă a unui drum de la nodul 1 la nodul 4, format doar din arce distincte?

a. 5
b. 6
c. 4
d. 7
Raspuns: B
2. Un graf neorientat cu nodurile numerotate de la 1 la 4 este reprezentat prin
matricea de adiacenţă alăturată. Care dintre afirmaţiile de mai jos este
adevărată pentru acest graf?
a. Graful este arbore
b. Graful nu este conex
c. Graful este ciclic
d. Graful are toate gradele nodurilor numere pare
Raspuns: A
Varianta 83
2. Se consideră graful orientat cu nodurile numerotate de la 1 la 5 şi arcele (2,1), (5,1),
(1,2), (3,2), (5,2), (4,3), (2,5), (4,5). Care este lungimea maximă a unui drum
de la nodul 4 la nodul 1, format doar din arce distincte?
a. 6
b. 5
c. 4
d. 7

Raspuns: B
3. Scrieţi matricea de adiacenţă a unui graf neorientat cu 6 noduri în care toate nodurile au
gradul 2 şi care are două componente conexe.
Raspuns:


Varianta 84
1. Se consideră graful neorientat cu nodurile numerotate de la 1 la 6 şi având muchiile
[1,2], [2,3], [2,5], [2,6], [3,4], [4,5], [4,6], [5,6]. Câte lanţuri , distincte şi de
lungime 3 există de la nodul 1 la nodul 4 în graful dat? Două lanţuri sunt distincte dacă
diferă prin cel puţin o muchie.
a. 2
b. 0
c. 4
d. 3

Raspuns: D
2. Un arbore cu 9 noduri, numerotate de la 1 la 9, este memorat cu ajutorul vectorului „de taţi”
t=(9,3,4,7,3,9,0,7,2). Mulţimea tuturor nodurilor de tip frunză este:
a. {8, 6, 1, 5}
b. {1, 6}
c. {8}
d. {1, 6, 8}
Raspuns: A
Varianta 85
1. Se consideră graful orientat cu vârfurile numerotate de la 1 la 7 şi arcele (1,2),
(1,7), (2,3), (3,2), (3,4), (4,3), (5,4), (5,6), (6,4), (7,6).Câte vârfuri din graful dat au gradul extern impar?

a. 4
b. 3
c. 1
d. 2
Raspuns: A
2. Care dintre următoarele afirmaţii este adevărată pentru graful neorientat având mulţimea
nodurilor X={1,2,3,4,5} şi mulţimea muchiilor U={[1,2], [1,5], [2,3], [2,4],
[3,4], [4,5]}?
a. Este graf hamiltonian, dar nu este eulerian.
b. Este graf eulerian, dar nu este hamiltonian.
c. Este şi graf hamiltonian şi graf eulerian.
d. Nu este graf hamiltonian, şi nici nu este graf eulerian
.
Raspuns: A
Varianta 82:
1. Se consideră graful orientat cu nodurile numerotate de la 1 la 5 şi arcele (1,2), (1,5),
(2,1), (2,3), (2,5), (3,4), (5,2), (5,4). Care este lungimea maximă a unui drum de la nodul 1 la nodul 4, format doar din arce distincte?
a. 5
b. 6
c. 4
d. 7
Raspuns: B
2. Un graf neorientat cu nodurile numerotate de la 1 la 4 este reprezentat prin
matricea de adiacenţă alăturată. Care dintre afirmaţiile de mai jos este
adevărată pentru acest graf?
a. Graful este arbore
b. Graful nu este conex
c. Graful este ciclic
d. Graful are toate gradele nodurilor numere pare
Raspuns: A
Varianta 83
2. Se consideră graful orientat cu nodurile numerotate de la 1 la 5 şi arcele (2,1), (5,1),
(1,2), (3,2), (5,2), (4,3), (2,5), (4,5). Care este lungimea maximă a unui drum
de la nodul 4 la nodul 1, format doar din arce distincte?
a. 6
b. 5
c. 4
d. 7
Raspuns: B
3. Scrieţi matricea de adiacenţă a unui graf neorientat cu 6 noduri în care toate nodurile au
gradul 2 şi care are două componente conexe.
Raspuns:
Varianta 84
1. Se consideră graful neorientat cu nodurile numerotate de la 1 la 6 şi având muchiile
[1,2], [2,3], [2,5], [2,6], [3,4], [4,5], [4,6], [5,6]. Câte lanţuri , distincte şi de
lungime 3 există de la nodul 1 la nodul 4 în graful dat? Două lanţuri sunt distincte dacă
diferă prin cel puţin o muchie.
a. 2
b. 0
c. 4
d. 3
Raspuns: D
2. Un arbore cu 9 noduri, numerotate de la 1 la 9, este memorat cu ajutorul vectorului „de taţi”
t=(9,3,4,7,3,9,0,7,2). Mulţimea tuturor nodurilor de tip frunză este:
a. {8, 6, 1, 5}
b. {1, 6}
c. {8}
d. {1, 6, 8}
Raspuns: A
Varianta 85
1. Se consideră graful orientat cu vârfurile numerotate de la 1 la 7 şi arcele (1,2),
(1,7), (2,3), (3,2), (3,4), (4,3), (5,4), (5,6), (6,4), (7,6).Câte vârfuri din graful dat au gradul extern impar?
a. 4
b. 3
c. 1
d. 2
Raspuns: A
2. Un arbore cu 9 noduri, numerotate de la 1 la 9, este memorat cu ajutorul vectorului „de taţi”
t=(9,3,4,7,3,9,0,7,2). Care este numărul minim de muchii care trebuie eliminate pentru ca lungimea celul mai lung lanţ, format din noduri distincte, cu o extremitate în
rădăcină să fie 3?
a. 4
b. 3
c. 2
d. 5
Raspuns: A
Varinta 86.ex 3:Scrieţi matricea de adiacenţă a arborelui cu 6 noduri, numerotate de la 1 la 6, definit prin următorul vector "de taţi": (0, 1, 1, 1, 3, 3).
Vatina 87.ex 3: Se consideră un arbore cu 6 noduri, numerotate de la 1 la 6,
reprezentat prin matricea de adiacenţă dată alăturat. Scrieţi toate
nodurile care pot fi alese ca rădăcină a arborelui astfel încât acesta
să aibă un număr maxim de frunze.
RASPUNS: 1,2.
Varianta 88.ex 3: Se consideră un arbore cu 6 noduri, numerotate de la 1 la 6,
reprezentat prin matricea de adiacenţă dată alăturat. Scrieţi toate
nodurile care pot fi alese ca rădăcină a arborelui astfel încât acesta
să aibă un număr minim de frunze
RASPUNS: 3,4,5,6.
Varianta 89. ex 3: Determinaţi ultima valoare (notată cu „?”) din vectorului „de taţi” (0, 1, 1, 2, 3, 3, ?) astfel încât arborele cu 7 noduri, numerotate de la 1 la 7, descris de acest vector, să aibă pe fiecare nivel n exact 2n noduri, nodul rădăcină fiind pe nivelul n=0, şi fiecare nod să aibă cel mult doi descendenţi. Scrieţi matricea de adiacenţă a arborelui astfel definit.
Varianta 90. ex 3: Se consideră un arbore cu 6 noduri, numerotate de la 1 la 6,
reprezentat prin matricea de adiacenţă dată alăturat. Scrieţi toate
nodurile care pot fi alese ca rădăcină a arborelui astfel încât acesta
să aibă un număr par de frunze.

RASPUNS: 1,2.
Vatina 87.ex 3: Se consideră un arbore cu 6 noduri, numerotate de la 1 la 6,
reprezentat prin matricea de adiacenţă dată alăturat. Scrieţi toate
nodurile care pot fi alese ca rădăcină a arborelui astfel încât acesta
să aibă un număr maxim de frunze.
RASPUNS: 1,2.
Varianta 88.ex 3: Se consideră un arbore cu 6 noduri, numerotate de la 1 la 6,
reprezentat prin matricea de adiacenţă dată alăturat. Scrieţi toate
nodurile care pot fi alese ca rădăcină a arborelui astfel încât acesta
să aibă un număr minim de frunze
RASPUNS: 3,4,5,6.
Varianta 89. ex 3: Determinaţi ultima valoare (notată cu „?”) din vectorului „de taţi” (0, 1, 1, 2, 3, 3, ?) astfel încât arborele cu 7 noduri, numerotate de la 1 la 7, descris de acest vector, să aibă pe fiecare nivel n exact 2n noduri, nodul rădăcină fiind pe nivelul n=0, şi fiecare nod să aibă cel mult doi descendenţi. Scrieţi matricea de adiacenţă a arborelui astfel definit.
Varianta 90. ex 3: Se consideră un arbore cu 6 noduri, numerotate de la 1 la 6,
reprezentat prin matricea de adiacenţă dată alăturat. Scrieţi toate
nodurile care pot fi alese ca rădăcină a arborelui astfel încât acesta
să aibă un număr par de frunze.
RASPUNS: 1,2.
Realizat de catre:
- Constantinescu Florin
- Totoc Traian
- Tigau Adrian
Subiecte pentru bac
Varianta 16
2. Un algoritm generează în ordine crescătoare toate numerele de n cifre, folosind doar cifrele 3, 5 şi 7. Dacă pentru n=5, primele 5 soluţii generate sunt 33333, 33335, 33337,
33353, 33355, precizaţi care sunt ultimele 3 soluţii generate, în ordinea generării.
Raspuns : (77773);(77775);(77777)
Varianta 17
2. Un algoritm generează în ordine descrescătoare toate numerele de 5 cifre, fiecare dintre ele având cifrele în ordine strict crescătoare. Ştiind că primele 5 soluţii generate sunt 56789, 46789, 45789, 45689, 45679, precizaţi care sunt ultimele 3 soluţii generate, în ordinea generării.
Raspuns: (12347); (12346); (12345)
Varianta 18
2. Un algoritm generează, în ordine lexicografică, toate şirurile alcătuite din câte n cifre binare
(0 şi 1). Ştiind că pentru n=5, primele 4 soluţii generate sunt 00000, 00001, 00010, 00011,
precizaţi care sunt ultimele 3 soluţii generate, în ordinea obţinerii lor.
Raspuns: 11101; 11110 ; 11111
Varianta 19
2. Un algoritm generează în ordine crescătoare, toate numerele de n cifre (n<9), cu cifre
distincte, care nu au două cifre pare alăturate. Dacă pentru n=5, primele 5 soluţii generate
sunt 10325, 10327, 10329, 10345, 10347, precizaţi care sunt următoarele 3 soluţii
generate, în ordinea obţinerii lor.
Raspuns: 10349; 10356; 10357
Varianta 20
2. Un algoritm generează în ordine descrescătoare, toate numerele de n cifre (n<9), cu cifrele
în ordine strict crescătoare, care nu au două cifre pare alăturate. Dacă pentru n=5, primele
5 soluţii generate sunt 56789, 45789, 45679, 45678, 36789, precizaţi care sunt
următoarele 3 soluţii generate, în ordinea obţinerii lor.
Raspuns: 35789; 35679; 35678
Varianta 21
1. Care din următoarele probleme referitoare la mulţimea de numere reale M={x1, x2, …, xn}
(n>1000) poate fi rezolvată cu un algoritm care are un număr minim de paşi? (4p.)
a. sortarea elementelor mulţimii M
b. generarea elementelor produsului cartezian M x M
c. determinarea elementului minim al mulţimii M
d. generarea tuturor permutărilor mulţimii M
Raspuns :c)determinarea elementului minim al mulţimii M
Varianta 22
1. In timpul procesului de generare a permutărilor mulţimii {1,2,…,n} prin metoda
backtracking, în tabloul unidimensional x este plasat un element xk (1≤k≤n). Acesta este
considerat valid dacă este îndeplinită condiţia:
a. xk∉{x1, x2, …, xk-1}
b. xk≠xk-1
c. xk∉{x1, x2, …, xn}
d. xk≠xk-1 şi xk≠xk+1
Raspuns: a)xk∉{x1, x2, …, xk-1}
Varanta 23
1. Algoritmul de generare a tuturor numerelor de 5 cifre nenule, fiecare având cifrele ordonate
strict crescător, este echivalent cu algoritmul de generare a: (6p.)
a. submulţimilor unei mulţimi cu 5 elemente
b. produsului cartezian a unor mulţimi de cifre
c. aranjamentelor de 9 elemente luate câte 5
d. combinărilor de 9 elemente luate câte 5
Raspuns:d) combinărilor de 9 elemente luate câte 5
Varianta 24
1. Generând şirurile de maximum 3 caractere distincte din mulţimea {A,B,C,D,E}, ordonate
lexicografic, obţinem succesiv: A, AB, ABC, ABD,…. Ce şir va fi generat după BAE? (4p.)
a. BCA
b. CAB
c. BC
d. BEA
Raspuns:a) BCA
Varianta 25
1. Un program citeşte o valoare naturală nenulă impară pentru n şi apoi generează şi afişează
în ordine crescătoare lexicografic toate combinaţiile formate din n cifre care îndeplinesc
- conţin doar valori pozitive sau nule;
- încep şi se termină cu 0;
- modulul diferenţei între oricare două cifre alăturate dintr-o combinaţie este 1.
Astfel, pentru n=5, combinaţiile afişate sunt, în ordine, următoarele: 01010, 01210. Dacă
se rulează acest program şi se citeşte pentru n valoarea 7, imediat după combinaţia
0101210 va fi afişată combinaţia: (4p.)
a. 0121210 b. 0123210 c. 0111210 d. 0121010
Raspuns:c) 0111210
Varianta 26
1. Pentru generarea numerelor cu n cifre formate cu elementele mulţimii {0,2,8} se
utilizează un algoritm backtracking care, pentru n=2, generează, în ordine, numerele
20,22,28,80,82,88. Dacă n=4 şi se utilizează acelaşi algoritm, care este numărul generat imediat după numărul
2008 ? (4p.)
a. 2002 b. 2020 c. 2080 d. 8002
Raspuns:b) 2020
Varianta 27
1. Pentru generarea numerelor cu n cifre formate cu elementele mulţimii {0,2,8} se
utilizează un algoritm backtracking care, pentru n=2, generează, în ordine, numerele
20,22,28,80,82,88.
Dacă n=4 şi se utilizează acelaşi algoritm, precizaţi câte numere generate sunt divizibile
cu 100?
a. 601 b. 100 c. 6 d. 10
Raspuns:c. 6
Varianta 28
1. Generarea tuturor combinaţiilor de trei litere mici ale alfabetului englez, se poate realiza cu
ajutorul unui algoritm echivalent cu cel de generare a:
a. produsului cartezian
b. combinărilor
c. aranjamentelor
d. permutărilor
Raspuns:a. produsului cartezian
Varianta 29
1. În câte dintre permutările elementelor mulţimii {‘I’,’N’,’F’,’O’} vocalele apar pe
poziţii consecutive?
a. 24 b. 6 c. 12 d. 4
Raspuns:c. 12
Varianta 30
1. Pentru generarea numerelor cu n cifre formate cu elementele mulţimii {0,4,8} se
utilizează un algoritm backtracking care, pentru n=2, generează, în ordine, numerele
Dacă n=4 şi se utilizează acelaşi algoritm, care este numărul generat imediat după numărul
4008 ?
a. 4040 b. 4004 c. 4080 d. 8004
Raspuns:a. 4040
Varianta 31
1. Având la dispoziţie cifrele 0, 1 şi 2 putem genera, în ordine crescătoare, numere care au
suma cifrelor egală cu 2 astfel încât primele 6 numere generate sunt, în această ordine: 2,
11, 20, 101, 110, 200. Folosind acelaşi algoritm se generează numere cu cifrele 0, 1, 2 şi
3 care au suma cifrelor egală cu 4. Care va fi al 7-lea număr din această generare ? (4p.)
a. 103 b. 301 c. 220 d. 130
Raspuns:c. 220
Varianta 32
1. În vederea participării la un concurs, elevii de la liceul sportiv au dat o probă de selecţie, în
urma căreia primii 6 au obţinut punctaje egale. În câte moduri poate fi formată echipa
selecţionată ştiind că poate avea doar 4 membri, aleşi dintre cei 6, şi că ordinea acestora în
cadrul echipei nu contează?
a. 24 b. 30 c. 15 d. 4
Raspuns:c. 15
Play Casino Games Online for Free at Chocolates Casino m88 m88 카지노 카지노 クイーンカジノ クイーンカジノ 10cric login 10cric login bet365 bet365 カジノ シークレット カジノ シークレット 카지노 카지노 planet win 365 planet win 365 우리카지노 마틴 우리카지노 마틴 695 The Best Sports Betting Sites and Bonuses 2021 - Acbet
RăspundețiȘtergere